Climate Matching: Seeking a Mediterranean-Like Climate in The US
Introduction:
I was recently tasked with a project with the goal of finding prospective locations with mediterranean like climates in the continental US. Ultimately, we wished to obtain a metric that quantifies similarities to our “ideal” mediterranean climate across points in the US. First and foremost though, is the issue of sourcing data. Luckily for us, NOAA’s NCDC API gives us a great deal of historical weather data to play with across thousands of points in the US. The second is identifying the type of data we need to obtain this metric. In the Koppen Classification scheme, climates are broken down by 4 measurements throughout the year. The maximum temperature \(T_{max}\), minimum temperature \(T_{min}\), average temperature \(T_{avg}\) and precipitation \(P\). These measurements are made available to us in the aforementioned API for all twelve months throughout the year. In the remainder of this article, I’ll highlight some methods and resources I used to identify locations with mediterranean-like climates. Furthermore, at the very end of the article I’ll include a neat PowerBI dashboard you can use to dig through the resulting data yourself.
Background:
In the Koppen climate classifications, a qualitative description of a mediterranean climate is one that has holds an average temperature in the winter months slightly above 0 degrees Celsius, with an average temperature in the summer months around 22 degrees celsius. There are different types of mediterranean climate sub-classifications, Csa, Csb, and Csc belonging to hot-summer mediterranean, warm-summer mediterranean, and cold-summer mediterranean climates respectively. For this project we’ll use a reference climate to compare against, so thorough knowledge of these sub-classifications schemes are not required. If you wish to find out more though, you can learn about them here .
Methods:
Sourcing Data
Obtaining Station Metadata
Before we begin collecting historical weather data, we need to collect a list of all weather stations available in NOAA’s API. Fortunately, there’s a package in R that makes interfacing with the API extremely easy. The package is called rnoaa, and you can learn more about it here . It’s important to note, that you must sign up for an API token to access the data through rnoaa, since it’s basically a wrapper for the API. To obtain the metadata of each individual station we’ll use the ncdc_stations() function in the package. This will give us meta-data about each station, such as it’s lat-long, data coverage, date of first and last measurements, elevation, name and ID. The ncdc_stations() returns a list of weather station meta-data near the proximity of a lat-long, with a default limit of 100 (you can specify the limit to be up to 1000). With some elementary programming, I repeatedly applied this function across a fine grid of points throughout the US and obtainied roughly 53k unique weather stations.
{library(rnoaa)
library(tidyverse)
library(magrittr)
library(rnoaa)
library(profvis)
## Outer grid bounds ##
max <- c(48, -122)
min <- c( 37.6, -129.0)
token = "Get-Your-Own"
## Inner Grid Bounds ##
dlat <- 1
dlong <- 2.5
changelat <- (max[1] - min[1])
changelong <- (max[2] - min[2])
iterlat <- (changelat/dlat + 0.5) %>% round(0)
iterlong <- (changelong/dlong + 0.5) %>% round( 0)
lat <- min[1]
long <- min[2]
### Initialize ###
stations.metadata <- ncdc_stations(datasetid = 'GSOM', extent = c(lat, long, lat + dlat, long + dlong), token = token )$data %>% as.data.frame()
for(i in 0:(iterlat - 1)){
for(j in 1:(iterlong- 1)){
long = long + dlong
print(paste0("lat - long: ", lat, " - ", long))
newframe <- as.data.frame(ncdc_stations(datasetid = 'GSOM', extent = c(lat, long, lat + dlat, long + dlong), limit = 900, token = token )$data)
print(newframe)
if(nrow(newframe) > 0){
stations.metadata <- rbind(stations.metadata, newframe)
}
pause(3)
}
long <- min[2]
lat = lat + dlat
}
}Let’s filter out duplicate rows and visualize the results:
library(RColorBrewer)
rf <- colorRampPalette(rev(brewer.pal(11,'Spectral')))
r <- rf(55)
usa <- map_data("usa")
ggplot() + geom_polygon(data = usa, aes(x = long, y = lat, group = group)) + stat_bin_2d(data = stations.metadata,aes(x = longitude, y = latitude), bins = 40, alpha = 0.4) + scale_fill_gradientn(colours=r)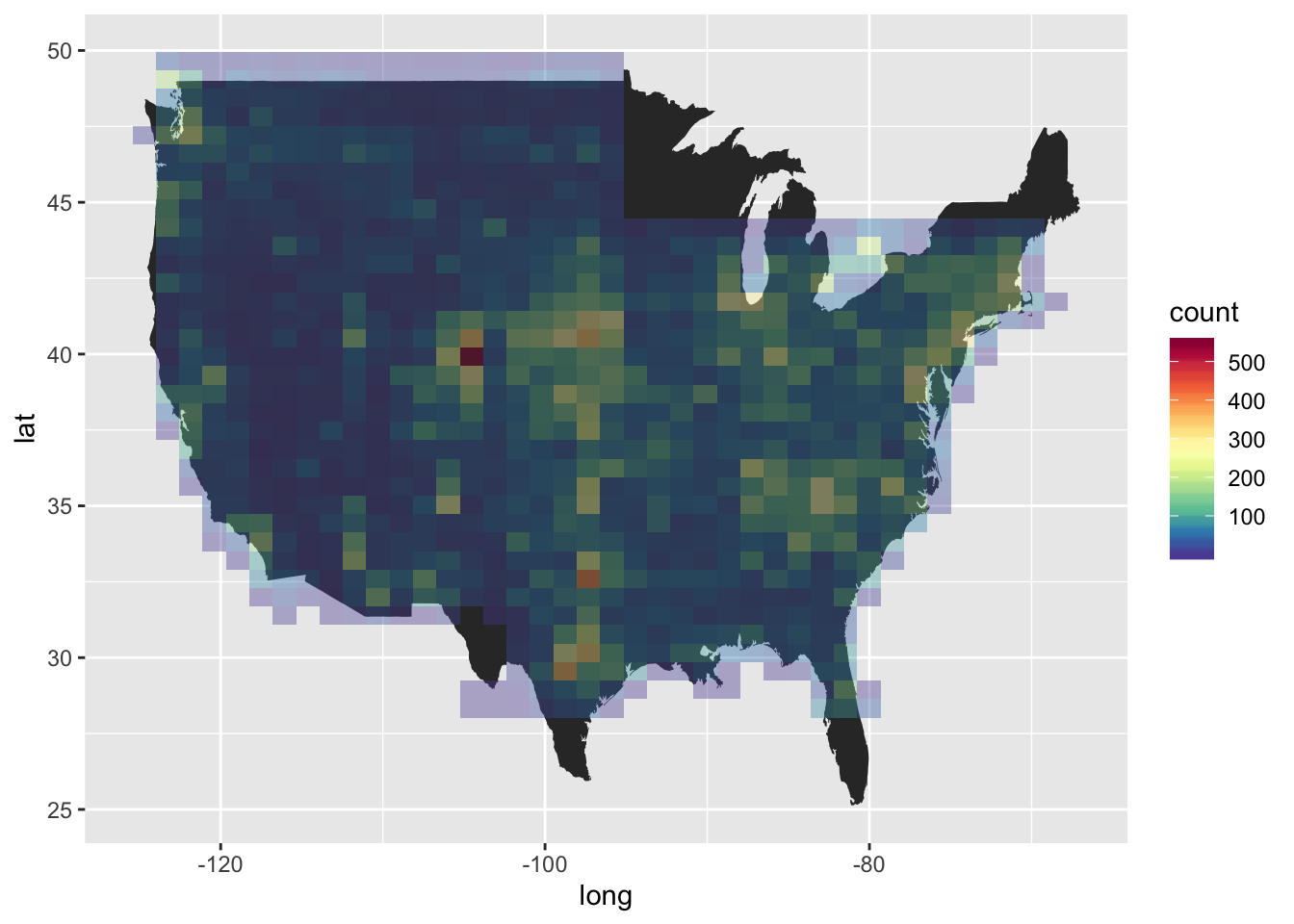
There seems to be data missing in southern Florida, along with Minnesota, Wisconsin and Massachusetts. We won’t bother with sourcing any meta-data from these locations though, since we know they possess extremely frigid winters, or very warm summers. For these reasons we’ll also filter out most of the midwest states,a couple of points outside the US, and weather stations that don’t contain any data within the past couple of years.
## filter out Non-US Stations:
stations.metadata %<>% unique()
stations.metadata %<>% filter(str_detect(name, "US"))
## filter out midwest states with severe freezes.
xlim <- c(-115.2,-82.3)
ylim <- c(37.14,53)
stations.metadata %<>% filter( !((longitude > xlim[1] & longitude < xlim[2]) & latitude > ylim[1]))
### keep stations with recent data
stations.metadata %<>% filter(mindate <= '2017-01-01' & maxdate >= '2018-12-01')
ggplot() + geom_polygon(data = usa, aes(x = long, y = lat, group = group)) + stat_bin_2d(data = stations.metadata,aes(x = longitude, y = latitude), bins = 40, alpha = 0.4) + scale_fill_gradientn(colours=r)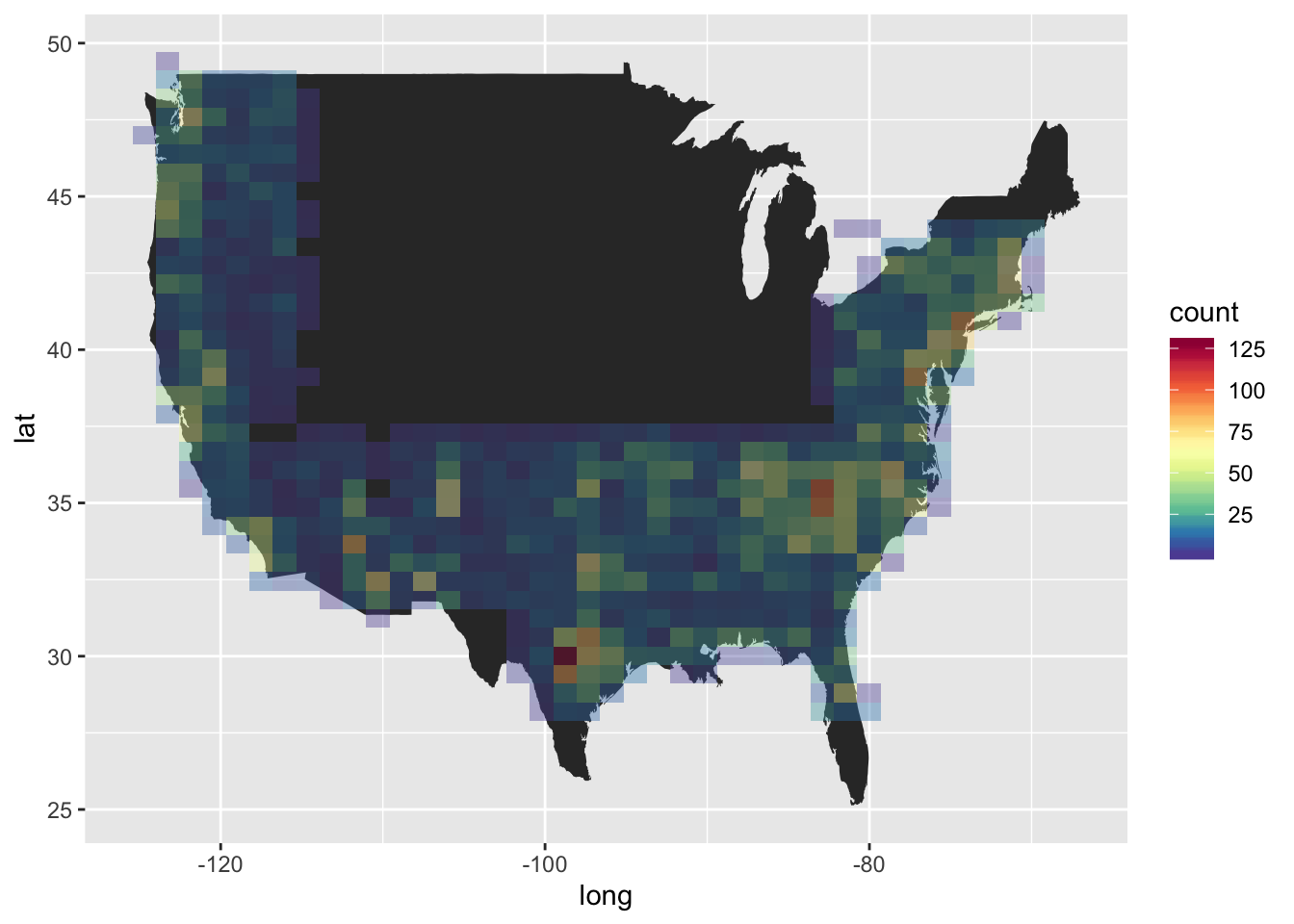
Obtaining Historical Weather Data
With the number of stations greatly reduced, we can go ahead and call NOAA’s API for the 2017 and 2018 monthly averages of \(T_{max}\), \(T_{min}\), & \(P\). We’ll also go ahead and assume \(T_{avg} = \frac{T_{max} + T_{min}}{2}\)
We iterate calls to the API and append rows only if values exist for the 3 variables in all 12 months of 2017. We can repeat the process for 2018 as well.
## Initialize dataframe
df <- ncdc(datasetid = 'GSOM', stationid = as.character(stations.metadata[44,7]), startdate = '2017-01-01',enddate = '2017-12-01', token = token, datatypeid = c("TMIN", "TMAX", "PRCP"), limit = 100)$data %>% .[,1:4] %>% as.data.frame() %>% mutate(date = str_replace(date,"T", " ")) %>% mutate(date = as.Date(ymd_hms(date))) %>% spread(date, value)
for (i in 1:nrow(stations.metadata)){
data <- ncdc(datasetid = 'GSOM', stationid = as.character(stations.metadata[i,7]), startdate = '2017-01-01',enddate = '2017-12-01', token = token, datatypeid = c("TMIN", "TMAX", "PRCP"), limit = 100)$data
nrow(data) %>% print()
i %>% print()
print("---------------------")
if (nrow(data) == 36){
## Append new rows
spreaded <-data %>% .[,1:4] %>% as.data.frame() %>% mutate(date = str_replace(date,"T", " ")) %>% mutate(date = as.Date(ymd_hms(date))) %>% spread(date, value) %>% print()
df <- rbind(df, spreaded)
}
## Pause to bypass API limit
pause(0.5)
}After saving each data frame as a CSV (in case something terrible happens), we can join the 2017 and 2018 dataframe, making sure to add a column denoting each year. We then edit the column names, to keep only the month number, with some quick stringr functions, and then reshape!
stationdat17 <- read.csv("../../../ClimateWS/WeatherMatching/weatherstationdatanoaa2017.csv", stringsAsFactors = F, header = T)[,-c(1)]
stationdat18 <- read.csv("../../../ClimateWS/WeatherMatching/weatherstationdata2018.csv", stringsAsFactors = F, header = T)[,-c(1)]
stationdat17$year <- "2017"
stationdat18$year <- "2018"
names(stationdat17) %<>% str_replace("X2017.", "") %>% str_replace(".01","")
names(stationdat18) %<>% str_replace("X2018.", "") %>% str_replace(".01","")
agghist <- rbind(stationdat17, stationdat18) %>% distinct()
names(agghist)[2] <- "id"
datapointscatter <- agghist %>% select(id, year) %>% distinct() %>% inner_join(stations.metadata, by = "id") %>% select(id,year, latitude, longitude) %>% ggplot() + geom_polygon(data = usa, aes(x = long, y = lat, group = group)) + geom_point(aes(x = longitude, y = latitude, color = year)) + ggtitle(paste0(agghist %>% nrow()/3," observations in ",agghist$id %>% unique() %>% length(), " unique locations")) + theme(plot.title = element_text(hjust = 0.5))
ggplotly(datapointscatter)Great, now that we have historical data for the past couple of years across 2500 distinct points we can start thinking of a metric that describes a similarity in climate. Let’s take a look at Barcelona’s average high temperature, low temperature, and precipitation.
### Desired climate values (Barcelona) in celcius and precip in mm ###
month <- c('01', '02','03','04','05','06','07','08','09','10','11','12')
TMAX <- c(15,15,17,20,23,27,29,29,26,23,18,15)
TMIN <- c(9,8,10,13,16,20,23,23,20,17,12,9)
PRCP <- c(34.9, 39.8, 76.2,48.7,57.8,27.5,39.3,26.7,70.2,90.1,71.4,23)
ideal <- as.data.frame(cbind(month, TMAX, TMIN, PRCP),stringsAsFactors = F)
ideal$TMAX %<>% as.numeric()
ideal$TMIN %<>% as.numeric()
ideal$PRCP %<>% as.numeric()
barcel2018 <- ideal %>% gather("Measurement", "Value", 2:4) %<>% ggplot(aes(x = month, y = Value, group = Measurement, color = Measurement)) + geom_line() + facet_wrap(~if_else(str_detect(Measurement, "T"), "TEMP (C)", "PRCP (mm)"), scale = "free_y") + ylab(" PRCP/TEMP (mm/C)")
ggplotly(barcel2018)While we are interested in the precipitation throughout the year, the most important criteria we need to consider are the \(T_{max}\) & \(T_{min}\) curves. Why is that? Well, let’s take a look at Barcelona’s precipitation profile throughout the year. It seems to have two distinct wet seasons in the late winter/early spring and late fall/early winter. High precipitation throughout the freezing winter months isn’t something we’re looking for. Barcelona however, never seems to reach a freezing point, so we could be more forgiving for high precipitation throughout the winter months.
Let’s look at another climate of interest, Teruel Spain:
### Desired climate values in celcius and precip in mm ###
month <- c('01', '02','03','04','05','06','07','08','09','10','11','12')
TMAX <- c(10,12,16,17,22,28,32,31,26,20,14,10)
TMIN <- c(-2,-1,1,3,7,11,13,14,10,6,1,-1)
PRCP <- c(17.2, 14.5, 23.5, 38.7, 53.2, 44.7, 25.5, 33.2, 35.7, 44.3, 27.5, 16)
idealteruel <- as.data.frame(cbind(month, TMAX, TMIN, PRCP),stringsAsFactors = F)
idealteruel$TMAX %<>% as.numeric()
idealteruel$TMIN %<>% as.numeric()
idealteruel$PRCP %<>% as.numeric()
teruel2018 <- idealteruel %>% gather("Measurement", "Value", 2:4) %<>% ggplot(aes(x = month, y = Value, group = Measurement, color = Measurement)) + geom_line() + facet_wrap(~if_else(str_detect(Measurement, "T"), "TEMP (C)", "PRCP (mm)"), scale = "free_y") + ylab(" PRCP/TEMP (mm/C)")
ggplotly(teruel2018)Teruel can be categorized as possessing “hot-summer” mediterranean climate, we can see that there is a brief dip under freezing for our minimum temperatures from December through February. The dip is very small though, so we’re not too concerned about it.
Let’s go ahead and calculate the RMSE of the fit against our ideal climate (Teruel). We’ll be obtaining the RMSE of \(T_{min}\), \(T_{max}\), \(T_{avg}\), and \(P\). We’ll go ahead and extract perform some elementary feature extraction we’d like to see. This will be the minimum average temperature throughout the year, minimum temperature recorded, total precipitation in the winter, and total precipitation in the summer.
Data transformation & feature extraction
### Desired climate values in celcius and precip in mm ###
### Declare df of Teruel ###
ideal <- idealteruel
ideal %<>% gather("datatype", "value", 2:4) %>% mutate(value = as.numeric(value))
## Data pipeline, find residuals of data points and then RMSE ###
## Numerical Measures ##
results <- agghist %>% gather("month", "value", 3:14) %>% inner_join(ideal, by = c("month", "datatype")) %>% mutate(res = (value.y - value.x)^2) %>% group_by(datatype, year, id) %>% summarize(res = sqrt(sum(res)/12)) %>% spread("datatype","res")
## precipitation in winter (mm)
winterprecip <- agghist %>% gather("month", "value", 3:14) %>% filter(datatype == "PRCP"& month %in% c("01","02","03", "10", "11","12")) %>% group_by( year, id) %>% summarize(winterprecip = sum(value))
## precipitation in summer (mm) ##
summerprecip <- agghist %>% gather("month", "value", 3:14) %>% filter(datatype == "PRCP"& month %in% c("05","06","07", "08", "11","12")) %>% group_by( year, id) %>% summarize(summerprecip = sum(value))
winttemps <- agghist %>% gather("month", "value", 3:14) %>% filter(datatype %in% c("TMAX", "TMIN") & month %in% c("01","02","11","12")) %>% group_by(year, id)%>%summarize(minwint = min(value), maxwint = max(value))
wintavgmin <- agghist %>% gather("month", "value", 3:14) %>% filter(datatype %in% c("TMAX", "TMIN") & month %in% c("01","02","11","12")) %>% group_by(year, month, id) %>% mutate(TAVG = sum(value)/2) %>% group_by(year,id) %>% summarize(minavg = min(TAVG))
#### Final Datasets ###
final.exp <- results %>% inner_join(winterprecip, by = c("year", "id")) %>% inner_join(summerprecip, by = c("year", "id")) %>% inner_join(winttemps, by = c("year", "id")) %>% inner_join(wintavgmin, by = c("year", "id")) %>% inner_join(stations.metadata, by = "id") ## Add Any Supplemental Measures
agghistresiduals.exp <- agghist %>% gather("month", "value", 3:14) %>% inner_join(ideal, by = c("month", "datatype")) %>% mutate(res = (value.y - value.x))
## Export final datasets
write.csv(final.exp, "WeatherMatching/csv/finalepteruel.csv", row.names = FALSE)
write.csv(agghistresiduals.exp, "WeatherMatching/csv/agghistteruel.csv", row.names = FALSE)Results
Now that we have all of our data, we can search for ideal locations by applying filters for all of our pertinent variables. Rather than repeatedly applying these filters, I went ahead and created a dashboard in Tableau that you should find further down, this allows you to filter through the data in real time! The top left geo-spatial plot is shaded by temp error, the lighter points containing less RMSE for \(T_{min}\) & \(T_{max}\), while the larger points contain more RMSE error for \(P\). Selecting any point on this plot, will isolate the location on the table, giving you the other calculated parameters, the top and bottom line plots on the right contain the residuals of the temperature throughout the year, and the temperature themselves. The topmost slider allows you to filter by the total temperature RMSE.
Further work
I have included the RMSE values for \(T_{min}\),& \(T_{max}\), and \(P\), but have omitted the RMSE for \(_{Tavg}\). I’m not too convinced this is something worth fitting though, since it wouldn’t address locations with extreme temperatures. You could include this in your model if you wish. Furthermore, I have excluded the RMSE for \(P\) in the dashboard below, as it cluttered the line plot and made it less intuitive to read. If you have any questions, concerns, or comments, don’t be scared to reach out to me on twitter, facebook or linked in. Thanks!